Quantum noise

Heisenberg-Langevin approach

This approach considers the system-reservoir interaction with a damping terms and quantum noise operators. These operators produce fluctuations. The equations take the form of Langevin equations. This method is used for the calculation of two-time correlation functions.

Brownian motion as a prototype

The original Langevin equation describes Brownian motion, the apparently random movement of a particle in a fluid due to collisions with the molecules of the fluid,

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): m\frac{d^{2}\mathbf{x}}{dt^{2}}=-\lambda \frac{d\mathbf{x}}{dt}+\boldsymbol{\eta}\left( t\right).

The degree of freedom of interest here is the position Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathbf{x}

of the particle, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): m
denotes the particle's mass. The force acting on the particle is written as a sum of a viscous force proportional to the particle's velocity (Stokes' law), and a noise term Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \boldsymbol{\eta}\left( t\right)
(the name given in physical contexts to terms in stochastic differential equations which are stochastic processes) representing the effect of the collisions with the molecules of the fluid. The force Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \boldsymbol{\eta}\left( t\right)
has a Gaussian probability distribution with correlation function

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \left\langle \eta_{i}\left( t\right)\eta_{j}\left( t^{\prime}\right) \right\rangle =2\lambda k_{B}T\delta _{i,j}\delta \left(t-t^{\prime }\right) ,

where Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): k_B

is Boltzmann's constant, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): T
is the temperature and Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \eta_i\left( t\right)
is the i-th component of the vector Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \boldsymbol{\eta}\left( t\right)

. The δ-function form of the correlations in time means that the force at a time Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): t

is assumed to be completely uncorrelated with it at any other time. This is an approximation; the actual random force has a nonzero correlation time corresponding to the collision time of the molecules. However, the Langevin equation is used to describe the motion of a "macroscopic" particle at a much longer time scale, and in this limit the Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \delta

-correlation and the Langevin equation become exact.

Another prototypical feature of the Langevin equation is the occurrence of the damping coefficient 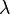$\lambda$ in the correlation function of the random force, a fact also known as |Einstein relation.

Basic system: single-mode field and reservoir of modes

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): H = \hbar \nu a^{\dagger} a + \sum \hbar \nu_k b^{\dagger}_k b_k + \hbar \sum g_k (b^{\dagger}_k a+ a^{\dagger} b_k)

The Heisenberg equations will take the form:

Formally solve the second equation and substitute it into the first one:

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.):  b_k(t)= b_k(0)e^{-i \nu_k t} -ig_k \int_{0}^{t} dt' a(t') e^{-i \nu_k (t-t')}

Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.):  \dot a_k(t)= -i \nu a - \sum_k g_k^2 \int_{0}^{t} dt' a(t') e^{-i \nu_k (t-t')} +f_a(t)

where Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): f_a(t)=-i \sum g_k b_k(0) e^{-i \nu_k t}

The noise operator varies rapidly since it contains all the reservoir frequencies Transfering annihilation operator into slowly varying:

... p283.

The system damping is determined from the fluctuating forces of the reservoir. The fluctuations induced by reservoir give rise to dissipation in the system.0