Spin Orbit Coupling
Contents
- 1 Creation of 2D SOC
- 2 References
Creation of 2D SOC
First realization
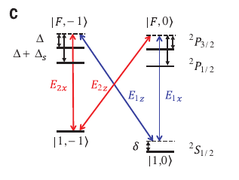
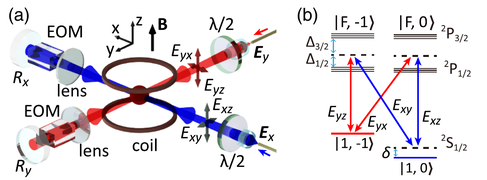
They realize 2D SOC in Rubidium atoms [1]. The engineered Hamiltonian: ![\hat H = \left[ \frac{\hbar k^2}{2m} +V_{latt}(x,z)\right]I+M_x(x,z)\sigma_x+M_y(x,z)\sigma_y+m_z\sigma_z](/images/math/4/1/4/414f9f7a32a1b443ec94ca399f2b4b56.png) , where Mx and My are periodic Raman coupling potentials, mz is a tunable Zeeman constant. The lattice potential is spin-independent, the hopping between nearest sights conserves the spin. Mx and My induce hopping that flips the spin. Lattice is created with a blue detuned (767 nm), they apply 49.6 G of bias magnetic field. They demonstrate:
, where Mx and My are periodic Raman coupling potentials, mz is a tunable Zeeman constant. The lattice potential is spin-independent, the hopping between nearest sights conserves the spin. Mx and My induce hopping that flips the spin. Lattice is created with a blue detuned (767 nm), they apply 49.6 G of bias magnetic field. They demonstrate:
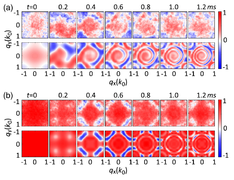
- 1D to 2D crossover (see figure B)
- They measure lifetime to be 300 ms, due to heating because of strong magnetic field.
- They demonstrate the spin distribution in the first Brillouin zone
- They prove nontrivial topology of the band. They find spin polarizations at four highly symmetric momenta.
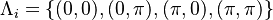 and the topological invariant is
and the topological invariant is ![\Theta=\prod_i{\text{sgn}[P(\Lambda_i)]}](/images/math/0/6/5/0654df5aa37dc786e5a7f42fe651698a.png)
Figure A: 4 blue counter-propagating fields form a lattice potential, red induces SOC.
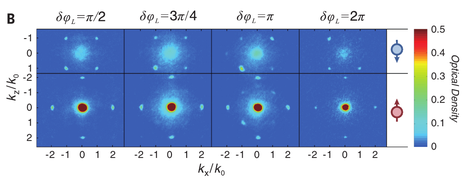
Figure B: Four peaks on axis Ox and Oy correspond to Bragg diffraction on an optical lattice (2k0 shifted). Four peaks on main diagonals correspond to Raman process (SOC) with shift of k0/sqrt(2).
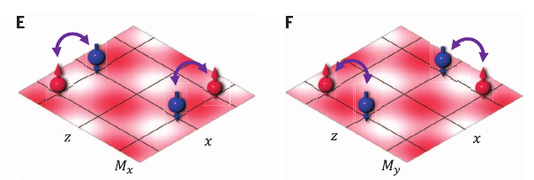
Figure E-F: grid crossing correspond to lattice node, where the atom is positioned.
Square lattice
The experimental realization is published here [2]. 2 orthogonal beams are sent back and forth to create a square lattice:
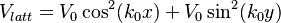 . The total Hamiltonian of the system reads as
. The total Hamiltonian of the system reads as 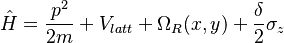 , where δ is the two-photon detuning. This Hamiltonian exhibits precise inversion and C4 symmetries. By tuning the phase between two beams δφ it is possible to transition from 1D to 2D SOC. For phases δφ=0, π, they demonsrate 1D SOC. For phases δφ=±π/2 they have symmetrical 2D SOC.
, where δ is the two-photon detuning. This Hamiltonian exhibits precise inversion and C4 symmetries. By tuning the phase between two beams δφ it is possible to transition from 1D to 2D SOC. For phases δφ=0, π, they demonsrate 1D SOC. For phases δφ=±π/2 they have symmetrical 2D SOC.
- They measure the lifetime of the BEC in 2D SOC, they find it to be 1-3s depending on the lattice depth.
- They measure the stripe and magnetic phases. They build the hystograms for different magnetizations, for the one they have a single peak at M=0 they call it a stripe phase. For the magnetic phase they have two sharp peaks at M=±1. The phase transition point is found as
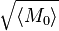 as a function of Ω, where they find a turning point.
as a function of Ω, where they find a turning point. - They measure band topology.
- They demonstrate signs of C4 symmetry
Uncover Topology by Quantum Quench Dynamics
In this [3] article the authors dynamically demonstrate the band topology. They demonstrate a ring structure during unitary spin evolution. Once again the engineered Hamiltonian: ![\hat H = \left[ \frac{p^2}{2m} +V_{latt}(x,y)\right]I+M_1(x,y)\sigma_x+M_2(x,y)\sigma_y+\frac{\delta}{2}\sigma_z](/images/math/6/c/e/6ce7ca2549829968a85e01baca2773bd.png) , where
, where 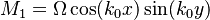 and
and 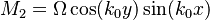 are periodic Raman coupling potentials, mz is a tunable Zeeman constant.
are periodic Raman coupling potentials, mz is a tunable Zeeman constant.
Experimental procedure
- Atoms are adiabatically loaded into 2D optical lattice (100 ms), the two-photon detuning is large, all atoms are in ↑ state
- the two-photon detuning is quickly (200 ns) switched to a near resonant value.
- a nonequilibrium evolution between ↑ and ↓ states takes place for a variable time t
- spin-resolved TOF measurement for various momenta q
They measured
- Ring pattern is best pronounced for δf=0, and it separates two regions with a phase transition
- For negative δf the ring surround M point (or edges of FBZ), for positive it surrounds Γ point (the center)
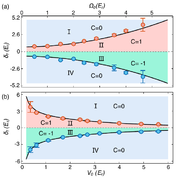
- The postquench band is topologically nontrivial with Chern number C=sgn(δf) for δf less than critical value (approximately 1).
- They find the Chern number
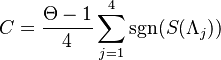 , where Λj are four symmetric momenta
, where Λj are four symmetric momenta 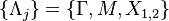
- They find the critical point δc by measuring the size of the ring
- Full topological phase diagram is much more precise than in previous works (Fig. c)
They demonstrate that a high-dimensional topological system (2D) can be characterized by a lower-dimensional invariant (1D ring).
Observing Topological Charges and Dynamical Bulk-Surface Correspondence with Ultracold Atoms
Autors of this [4] work question how to measure topological indices. As an example they give 1D winding number measured by Bloch's group and Chern numbers measured by this group previously. Another approach to characterize the topological phases dynamically, inducing quench evolution (see above). Their work is based on this theoretical proposal [5]. They dynamically detect topological charges of monopoles in momentum space.
Experimental setup
They added one more EOM. They could perform quenches with respect to all quantization axis. Thus they can extract the complete topological information by measuring only a single spin component. Along z they change two-photon detuning, along x and y they change Raman potential symmetry. For all quenches the postquench Hamiltonian is the same.
Experimental sequence
- Prepare atoms slightly above condensation
- Adiabatically (100 ms) load into the Raman lattice
- Change phases between lasers to exchange (0, π/2) ↔ (π/2, π/2) within 2 us
- atoms are out of equilibrium and evolve under postquench Hamiltonian
- TOF measurement, they plot spin textures
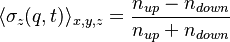
Measurement results
- The bulk topology can be characterized by the total topological charges in the region enclosed by band inversion surface. They list three universal criteria for drawing the boundary curves.
- Bulk-boundary correspondence in a real space has an analogue in momentum space: a dynamical bulk-surface correspondence. Which means that the bulk topology can be characterized by the dynamical topological pattern of lower dimension. They demonstrate the emergent dynamical field, the winding number of this field counts the topological charges.
Experimental observation of dynamical bulk-surface correspondence for topological phases
[6].
References
- ↑ Science, vol 354, ISSUE 6308
- ↑ PRL 121, 150401 (2018)
- ↑ Uncover Topology by Quantum Quench Dynamics, PRL 121, 250403 (2018)
- ↑ "Observing Topological Charges and Dynamical Bulk-Surface Correspondence with Ultracold Atom", PRL 123, 190603, 2019
- ↑ Dynamical detection of topological charges, PRA 99, 053606 (2019)
- ↑