EOM

EOM Kazan

Company Qubig produces eom PS3D-BC

$\delta \nu =FSR \frac{}{2\pi\lambda}\delta V$ 

Parameter	MIN	TYP	MAX	units
Bandwidth	DC		200	MHz
Maximum voltage			500	V
$V_\pi \, DC$			1	kV

Alignment procedure of intracavity EOM

1. First of all make sure, that the power @ 606 nm is larger than 480 mW in linear regime.
2. Put the IRISes along the optical path of the intracavity beam.
3. Block M4 mirror with the white paper. The fluorescence spot should be visible on it.
4. Insert an EOM into the cavity. The resulted the fluorescence spot on the white paper should be similiar to the original one as much as possible.

Problems

The generated mode is elliptical and the laser wouldn't generate if we tighten the iris below 3mm. After realignment of birefringent filter the problem seems to be redundant.

Attempts

1. During the first attempt in ring configuration we didn't get 606 nm. The only we got was 380mW @ 580nm and ~100 mW @593 nm.
2. During the second attempt in linear configuration we got 606 nm generation with the EOM and ~50% reduction in the power 480mW -> 250mW.
3. During the third attempt in linear configuration we got 606 nm generation with the EOM we got and ~50% reduction in the power 450mW -> 230mW.
4. Attempts to get 606 nm in ring configuration with EOM starting from the linear configuration with EOM were not successful. Final generation were still @ 580nm.

EOM Calgary

We bought a 10 GHZ phase modulator NIR-MPX80 from iX-Blue. The material is lithium niobate, characteristics are

Parameter	MIN	TYP	MAX	units
Wavelength	780	850	890	nm
Insertion loss		3.5	4.5	dB
Electro-optic bandwidth	10	12		GHz
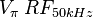
$V_\pi \, RF_{50kHz}$		4	5	V

Absolute maximum ratings:

Parameter	MAX	units
RF input power	28	dBm
Optical input power	14	dBm

How to find modulation depth from these parameters?

Let's assume we apply the optical wave with frequency 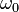$\omega_0$ and amplitude 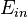$E_{in}$ and modulate the EO crystal with RF frequency 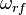$\omega_{rf}$ The output of EOM is described by the following expression:

$E_{out}= E_{in} e^{i\omega_o t +\beta \cos (\omega_{rf}t+\phi) } = E_{in} e^{i\omega_o t} \left( J_{0}(\beta) +\sum_{k=1} J_{k}(\beta) e^{ik\omega_{rf}} + (-1)^{k} J_{-k}(\beta) e^{-ik\omega_{rf}} \right)$

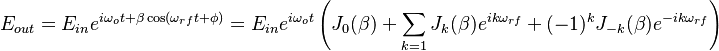
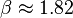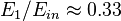Thus the maximum intensity of the first sideband is reached at $\beta \approx 1.82$, $E_{1}/E_{in} \approx 0.33$.

Thus by varying applied rf power and finding maximum it is possible to translate it into modulation depth index.