MOT
Contents
Light induced force
Maxwell in 19th century proposed that radiation has momentum. So the laser light effects not only internal degrees of freedom of an atom, but as well can change atomic motional states. We will use semiclassical description, in the rotating wave approximation (RWA) the atom-laser interaction: 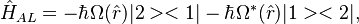 where the laser amplitude and phase are written in a form
where the laser amplitude and phase are written in a form 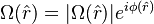 The force can be represented by
The force can be represented by ![{\textstyle \hat F = - [\nabla, \hat H (\hat r)] = \hbar \nabla \Omega(\hat r) | 2 ><1| + \hbar \nabla \Omega^{*}(\hat r) | 1 ><2|,}](/images/math/1/2/1/121854bd1d0664acc137db6fd56b7bd7.png) The average force
The average force 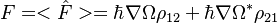 , which can be rewritten in a simple form:
, which can be rewritten in a simple form: 
Dipole force
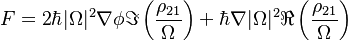 force consists of two components dissipative and reactive.
In the limit of large detunings
force consists of two components dissipative and reactive.
In the limit of large detunings 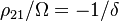 , so the response is almost purely reactive:
, so the response is almost purely reactive: 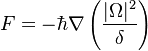
Dissipative force
Doppler cooling limit
Magneto-optical trap.
Specific techniques
Sisyphus cooling
Sisyphus cooling limit
Dark spot MOT
2D MOT
The rectangular magnetic coils used in the experiment have dimensions 40x85 mm and have 45 turns each. During loading phase the magnetic field gradient was 37.5 G/cm In this article they aimed to get highest OD possible. They optimised both the static loading of the MOT through geometry, a spatial dark spot and optical de-pumping, followed by a compression phase using a temporal dark spot.
"An ultra-high optical depth cold atomic ensemble for quantum memories. Sparkles, Buchler"
Here people used rectangular coils without any additional changes in the set-up of a regular 3D Mot. They achieved 2.7 times increase of OD. With the atom number of 7.2× 10^8 in the cigar-type MOT, we achieved an OD of the atom cloud of about 32 for the |5S1/2,F = 1> → |5P3/2,F' = 2> transition of the probe field. The transition has the saturation intensity I0 of 5.8 mW/cm2 [38], which is defined such that I/I0 = 2(Ω/Γ)2 where I and Ω are the intensity and the Rabi frequency of the laser field. With the atom number of 1.16× 10^9 in the conventional MOT, the OD of the atom cloud was 12.In the conventional MOT, the optimum axial magnetic field gradient and the trapping field detuning were 15 G/cm and 3.3Γ. The size of the atom cloud is about 2.7 ×2.9 × 2.7 mm3. In the cigar-type MOT, the optimum transverse magnetic field gradient and the trapping field detuning are 12 G/cm and 3.0Γ. The size of the cigar-shaped atom cloud is about 1.0 × 1.8 × 7.4 mm3.
"Using a pair of rectangular coils in the MOT for the production of cold atom clouds with large optical density Ite A. Yu"
Capture velocities
Temperatures for Rubidium atoms
Doppler cooling limit gives  . Than the speed of an individual atom is:
. Than the speed of an individual atom is:

The time it takes for an atom to pass the cavity mode: 
| Type of cooling | T_{limit}, [K] | V, [cm/s] | t, [ms] |
|---|---|---|---|
| doppler | 146 | 16.6 | 0.6 |
| Sisyphus | 10 | 5 | 1.8 |
MOT expansion
We have setup next experimental sequence to measure cold atomic cloud expansion after we switch off beams and magnetic coils. For the pulsed regime we use next code, where each step is described in comments:
1 #define CLUSTERmot (1<<2) | (1<<7) // repumper is 2, cool is 7
2 // repeats in the loop:
3 PIOC->PIO_SODR = CLUSTERmot | (1<<4); // C4 coils, CLUSTERmot correponds to
4 delay(500); // MOT is on for 500 ms
5 PIOA->PIO_CODR = CLUSTERsa; // we switch off our trigger, it needs to be on for at least 100 ms judging from specification of u-eye camera
6 PIOC->PIO_CODR = (1<<4); // turn of coils after 500 ms time of atoms collection
7 delayMicroseconds(50); // coils are switched before cool and repump, 50us
8 PIOC->PIO_CODR = CLUSTERmot; // we switch off cooling and repumping
9 delayMicroseconds(750); // we have an adjustable delay here, for the mot to expand
10 PIOA->PIO_SODR = CLUSTERsa; // we trigger camera at this moment
11 PIOC->PIO_SODR = CLUSTERmot ; // we have to switch both beams in order to see fluorescence on a camera
12 delayMicroseconds(100); // we keep them on for a time of exposure (the minimal exposure time is 71 us)
13 PIOC->PIO_CODR = CLUSTERmot ; // we switch off both lasers for some reason (no reason)
To trigger camera we send trigger directly form an Arduino Due (which has 3.3V logic) and it works. On the computer we record a video with 100% resolution, and after we cut into frames with VLC-player:
- Tools-> Prefereces -> Input/Codecs -> Show settings(all, left lower coner)
- scroll to Video -> Filters, place check mark next to "Scene video filter"
- choose Video -> Filters -> Scene filter set required path and press save.
- run your video
All files are here: ...\Calgary_Cold_atoms\MOT\MOT_expand We analyze photos in Mathematica and fit the MOT form with an ellipse. We average over 20-30 shots, and we have two different directions to observe. In a direction orthogonal to gravitational field we assume an uniform motion with an initial speed.
Our data gives averaged velocity of 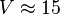 cm/s. Than the temperature of our cloud is:
cm/s. Than the temperature of our cloud is:
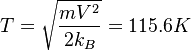
Loading time
We have measured loading time of our atomic cloud.
List of cites
- Lily's notes
- Atomic physics, Christopher J. Foot
- smth