Optical depth
Jump to navigation
Jump to search
Mathematical background
The spectral optical depth of a cloud of atoms can be calculated from the quantum-mechanical properties of the atoms and is given by:
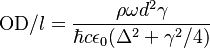 ,
where
,
where
- l is the length of the medium
- ρ is the density of atoms;
- ω is the frequency of the beam;
- d is the transition dipole moment;
- γ the natural linewidth of the transition.
- c is the speed of light;
- ħ is Planck's constant;
- ε0 is the vacuum permittivity;
- Δ the detuning of the laser from the atomic resonance;
for a detailed calculation please see (Two level atom in a free space, semi-classical description, Beer law)
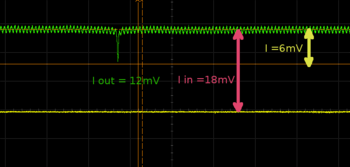
Experimental result
The data was taken on 18th July 2016. Optical depth measurement. We send weak less than 3uW beam from a side (MBR laser in our case), we set the waist around 200um to be overlapped with the cold atomic cloud. Scanning the laser through the resonance we observed absorption deep.
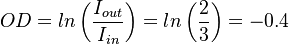
Knowing this we can find the density of the atomic cloud and the number of atoms:
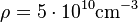 and
and  Constants used in calculation:
Constants used in calculation:
| OD | l, [mm] | ω, [THz] | d, | γ, [Hz] | ħ | ε0 |
|---|---|---|---|---|---|---|
| 0.4 | 1 | 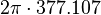 |
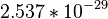 |
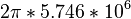 |
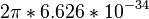 |
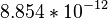
|