Topology

Spielman's review.

Berry phase

Direct measurement of the Zak phase in topological Bloch bands

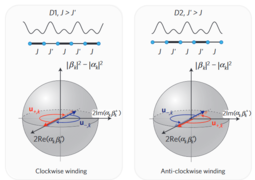
They work with 1D dimerized optical lattice (or as they call it a superlattice), which leads to the Rice-Mele Hamiltonian: 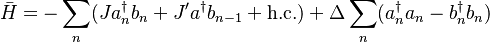$\bar H = -\sum_n(Ja^\dagger_n b_n+J'a^\dagger b_{n-1}+\text{h.c.})+\Delta\sum_n(a^\dagger_n a_n-b^\dagger_n b_n)$. If Δ is tuned to be equal then the system corresponds to the Su-Schrieffer-Heeger (SSH) model, which has two topologically distinct phases. The Zak phase difference between them is equal to π. The Zak phase is a gauge dependent quality, although the Zak phase difference of the two dimerizations is uniquely defined. Total phase obtained by a particle moved through the Brillouin zone has three contributions: geometric phase (Zak), dynamical phase (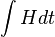$\int{H dt}$), and a phase due to Zeeman energy.

Experimental procedure

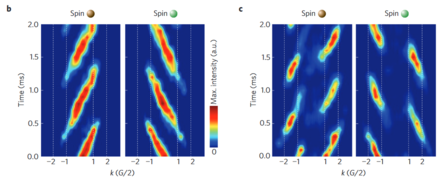
• By conrolling phase between two standing-wave lasers they were able to tune across phase transition.

1. prepare atoms in |↓, k=0> state
2. apply a π/2 pulse to have a superposition of ↑ and ↓,
3. the force created by the gradient of a magnetic field acts in opposite directions on two spins, thus superposition evolves into $|\uparrow,k>+e^{i\phi}|\downarrow,-k>$
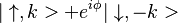
4. To eliminate Zeeman phase from the measurement a spin-echo π is applied, D1 changed to D2
5. Spins evolve in the upper band, until they return to k=0
6. π/2 is applied to interfere two spin components, the final phase measured is φ(Zak, D1)-φ(Zak, D2)

• 

  A. Two phases

• 

  B. Phases measurement