Difference between revisions of "Topology"
Jump to navigation
Jump to search
| (One intermediate revision by the same user not shown) | |||
| Line 9: | Line 9: | ||
# prepare atoms in |↓, k=0> state | # prepare atoms in |↓, k=0> state | ||
# apply a π/2 pulse to have a superposition of ↑ and ↓, | # apply a π/2 pulse to have a superposition of ↑ and ↓, | ||
| − | # the force created by the magnetic field acts in opposite directions, thus superposition evolves into <math>|\uparrow,k>+e^{i\phi}|\downarrow,-k></math> | + | # the force created by the gradient of a magnetic field acts in opposite directions on two spins, thus superposition evolves into <math>|\uparrow,k>+e^{i\phi}|\downarrow,-k></math> |
# To eliminate Zeeman phase from the measurement a spin-echo π is applied, D1 changed to D2 | # To eliminate Zeeman phase from the measurement a spin-echo π is applied, D1 changed to D2 | ||
# Spins evolve in the upper band, until they return to k=0 | # Spins evolve in the upper band, until they return to k=0 | ||
| Line 15: | Line 15: | ||
<gallery mode="packed-hover"> | <gallery mode="packed-hover"> | ||
| − | File:Berry 20200224 1.PNG | Two phases | + | File:Berry 20200224 1.PNG | A. Two phases |
| − | File:Berry 20200225 2.PNG | Phases measurement | + | File:Berry 20200225 2.PNG | B. Phases measurement |
</gallery> | </gallery> | ||
[[Category:BEC]] | [[Category:BEC]] | ||
Latest revision as of 14:09, 2 March 2020
Spielman's review.
Berry phase
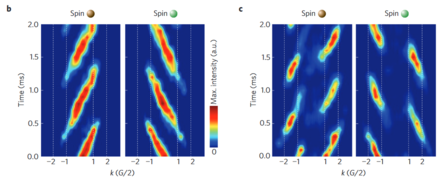
Direct measurement of the Zak phase in topological Bloch bands
They work with 1D dimerized optical lattice (or as they call it a superlattice), which leads to the Rice-Mele Hamiltonian:
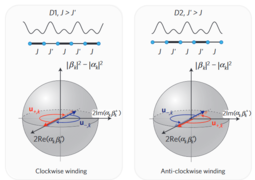
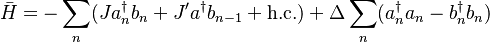 . If Δ is tuned to be equal then the system corresponds to the Su-Schrieffer-Heeger (SSH) model, which has two topologically distinct phases. The Zak phase difference between them is equal to π. The Zak phase is a gauge dependent quality, although the Zak phase difference of the two dimerizations is uniquely defined. Total phase obtained by a particle moved through the Brillouin zone has three contributions: geometric phase (Zak), dynamical phase (
. If Δ is tuned to be equal then the system corresponds to the Su-Schrieffer-Heeger (SSH) model, which has two topologically distinct phases. The Zak phase difference between them is equal to π. The Zak phase is a gauge dependent quality, although the Zak phase difference of the two dimerizations is uniquely defined. Total phase obtained by a particle moved through the Brillouin zone has three contributions: geometric phase (Zak), dynamical phase (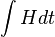 ), and a phase due to Zeeman energy.
), and a phase due to Zeeman energy.
Experimental procedure
- By conrolling phase between two standing-wave lasers they were able to tune across phase transition.
- prepare atoms in |↓, k=0> state
- apply a π/2 pulse to have a superposition of ↑ and ↓,
- the force created by the gradient of a magnetic field acts in opposite directions on two spins, thus superposition evolves into
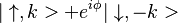
- To eliminate Zeeman phase from the measurement a spin-echo π is applied, D1 changed to D2
- Spins evolve in the upper band, until they return to k=0
- π/2 is applied to interfere two spin components, the final phase measured is φ(Zak, D1)-φ(Zak, D2)