Difference between revisions of "Topology"
Jump to navigation
Jump to search
| Line 2: | Line 2: | ||
==Berry phase== | ==Berry phase== | ||
===Direct measurement of the Zak phase in topological Bloch bands=== | ===Direct measurement of the Zak phase in topological Bloch bands=== | ||
| − | They work with 1D dimerized optical lattice, which leads to the Rice-Mele Hamiltonian: | + | They work with 1D dimerized optical lattice (or as they call it a superlattice), which leads to the Rice-Mele Hamiltonian: |
| − | <math>\bar H = -\sum_n(Ja^\dagger_n b_n+J'a^\dagger b_{n-1}+\text{h.c.})+\Delta\sum_n(a^\dagger_n a_n-b^\dagger_n b_n)</math>. If Δ is tuned to be equal then the system corresponds to the Su-Schrieffer-Heeger model. | + | <math>\bar H = -\sum_n(Ja^\dagger_n b_n+J'a^\dagger b_{n-1}+\text{h.c.})+\Delta\sum_n(a^\dagger_n a_n-b^\dagger_n b_n)</math>. If Δ is tuned to be equal then the system corresponds to the Su-Schrieffer-Heeger (SSH) model, which has two topologically distinct phases. The Zak phase difference between them is equal to π. |
<gallery mode="packed-hover"> | <gallery mode="packed-hover"> | ||
File:Berry 20200224 1.PNG | Two phases | File:Berry 20200224 1.PNG | Two phases | ||
</gallery> | </gallery> | ||
[[Category:BEC]] | [[Category:BEC]] | ||
Revision as of 17:27, 24 February 2020
Spielman's review.
Berry phase
Direct measurement of the Zak phase in topological Bloch bands
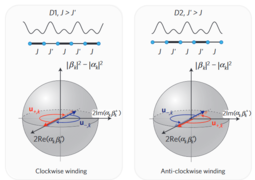
They work with 1D dimerized optical lattice (or as they call it a superlattice), which leads to the Rice-Mele Hamiltonian:
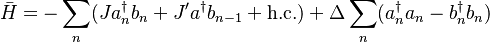. If Δ is tuned to be equal then the system corresponds to the Su-Schrieffer-Heeger (SSH) model, which has two topologically distinct phases. The Zak phase difference between them is equal to π.
Two phases
