Cooperativity
The square of the coupling constant is
 where d is a dipole moment matrix coefficient,
where d is a dipole moment matrix coefficient, 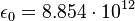 F/m,
F/m, 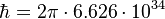 . The transition frequency for Rb87 D1 line is
. The transition frequency for Rb87 D1 line is 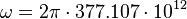 . The mode volume we assume to be
. The mode volume we assume to be  , where w is the waist, l is the cavity length. Thus the cooperativity is
, where w is the waist, l is the cavity length. Thus the cooperativity is 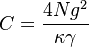 , the number of atoms could be found in Optical_depth. The comparison between our measurement on D1 line and Bimbard's measurement on D2 line, closed transition.
, the number of atoms could be found in Optical_depth. The comparison between our measurement on D1 line and Bimbard's measurement on D2 line, closed transition.
| C | dipole moment, d |  [MHz] [MHz]
|
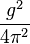
|
 [MHz] [MHz]
|
 [MHz] [MHz]
|
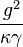
|
Number of atoms | Finesse | |
|---|---|---|---|---|---|---|---|---|---|
| our | 10 | 0.0138 | 5.746 | 15 | 2.2*10^-6 | 1.13*10^6 | 100 | ||
| Bimbard | 10 | 0.016 | 5.746 | 15 | 2.98*10^-6 | 0.8*10^6 | |||
| Bimbard article | 15 ( ) ) |
0.3* | D1 line | 10 | 0.0015 | 10^4 | 120 |
- found from other values from article
Cooperativity measurement
To overlap atomic cloud with a cavity mode and characterize an interaction strength, we measured the cooperativity parameter mentioned above (the ratio between the strengths of coherent and incoherent processes). We sent two lasers into the cavity. One of them was an MBR laser (violet colour on a picture \ref{fig:coop_measurement}). It passed through an acousto-optic modulator (AOM) in order to achieve two beams with different frequencies. The zeroth order beam served as a local oscillator (LO) for a heterodyne measurement. The first order was sent into the cavity to probe the atomic cloud. Thus it was set to be on resonance with Rb 87 D1 line, " ". When it leaks out from the cavity it reflects into a heterodyne detector. The second laser is homemade ECDL (yellow color on a picture \ref{fig:coop_measurement}) and is used to lock the cavity frequency via PDH technique \citep{drever1983laser} while being phase-locked to MBR by homemade lock \citep{macrae2009phaselock}. There are two requirements on ECDL central frequency. The laser should not effect the atoms and at the same time it should be in resonance with the cavity. Simultaneously cavity itself should be in resonance with the probe laser. Thus we lock ECDL to MBR laser 2 FSRs away (6.8 GHz). After these preliminary steps we acquire data points
". When it leaks out from the cavity it reflects into a heterodyne detector. The second laser is homemade ECDL (yellow color on a picture \ref{fig:coop_measurement}) and is used to lock the cavity frequency via PDH technique \citep{drever1983laser} while being phase-locked to MBR by homemade lock \citep{macrae2009phaselock}. There are two requirements on ECDL central frequency. The laser should not effect the atoms and at the same time it should be in resonance with the cavity. Simultaneously cavity itself should be in resonance with the probe laser. Thus we lock ECDL to MBR laser 2 FSRs away (6.8 GHz). After these preliminary steps we acquire data points 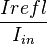 . The presence of the atoms will affect reflected intensity. Non-zero imaginary part of susceptibility increases intra-cavity losses, while the real part shifts resonance frequency. We estimated our cooperativity to be $C \approx 10$.
. The presence of the atoms will affect reflected intensity. Non-zero imaginary part of susceptibility increases intra-cavity losses, while the real part shifts resonance frequency. We estimated our cooperativity to be $C \approx 10$.
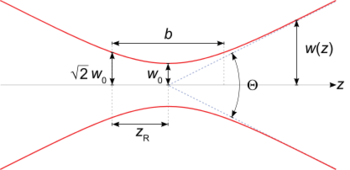
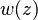 as a function of the axial distance
as a function of the axial distance 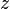 .
.  : beam waist;
: beam waist; 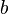 : confocal parameter;
: confocal parameter; 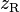 : Rayleigh length;
: Rayleigh length;  : total angular spread
: total angular spread